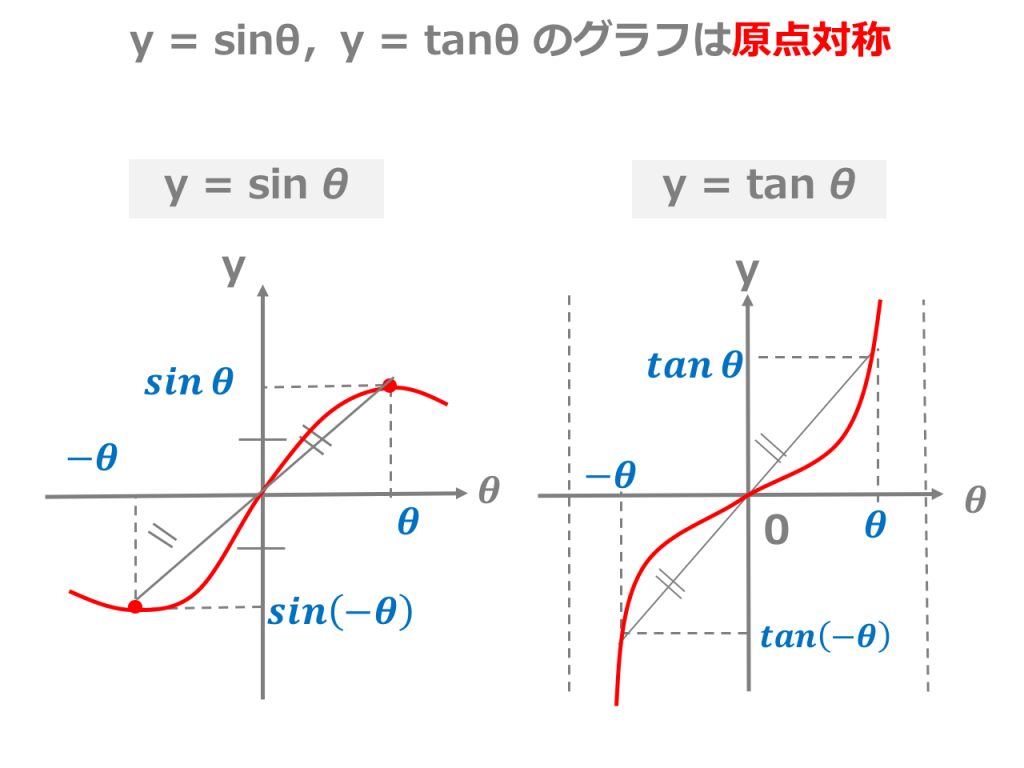
Nov 02, 19 · 3333 (グラフの準備:漸近線の求め方 (無理関数)) 2 2,718 ビュー このページを評価 (6 投票) 見て頂いてありがとうございます. 見てもらうために作成しておりますので,どんどん見てください. ★の数は優先度です.★→★★→★★★ の順に取り組み最大値、最小値、変曲点 MATLAB コマンドの表示 この例では、Symbolic Math Toolbox を使った解析的および数値的な技法により関数の極値を求める方法を説明します。 1 次導関数関数の局所的最小値および局所的最大値を求める 2 次導関数関数の変曲点を求めるMar 06, 21 · 同様に(または周期性から) x = π 2 (2 n 1) x=\dfrac{\pi}{2}(2n1) x = 2 π (2 n 1) ( n n n は任意の整数)という直線は y = tan x y=\tan x y = tan x の漸近線 であることが分かります。 グラフを描く際には漸近線は点線で描くとよいでしょう。

漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学
漸近線 求め方 tan
漸近線 求め方 tan-Jun 02, 19 · ランダウの記号を用いて f ( x) = ∑ k = 0 n f ( k) ( 0) k!Mar 11, 21 · tanxと1/tan xの微分公式のいろんな証明 一次近似の意味とよく使う近似公式一覧 デカルトの葉線の漸近線と面積 チェザロ平均の性質と関連する東大の問題 逆関数の微分公式を例題と図で理解する tanxの高階微分とマクローリン展開 増減表の書き方



3分でわかる 三角関数のグラフの描き方 合格サプリ
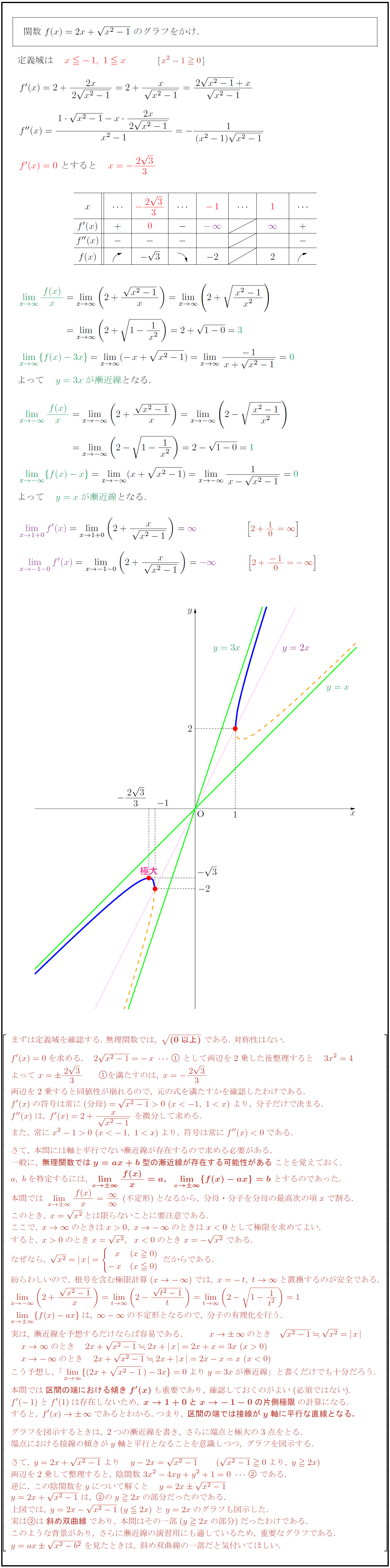
1xn = ス ス ス@ ス ス ス ス@ スA ス@ limx→−0limii e 1xn = 0 ス@ ス ス ス ス@ スC ス@ スA ス ス スQ ス゚撰ソス スフ包ソス ス ス ス ス ス ス x = 0 ス@ ス ス ス ス@ ス ス ス@ ( スC スヘ漸 ス゚撰ソス スニはなゑソスネゑソス) ス スx ス ス ス} ス ス スフとゑソス スフ漸 ス゚撰ソス ス ス ス@ limx→ ス} ス スlimii e 1xn = 1May 08, 21 · 漸近線を見出すことは、曲線の概形をつかむ一助となる。 特に、座標平面における関数に対しては、そのグラフの漸近線の方程式は(存在の可否も含めて)求め方が確立されている。関数のグラフの接線の極限が存在するならばそれは漸近線に等しい 。軸に平行でない漸近線の求め方2STEP ある関数 が 軸に平行でない直線 を漸近線に持つとき、以下3STEPで求めます。 STEP1 の極限を調べる→傾きチェック ある関数 が直線 を漸近線に持つとき、その距離はどこまでいっても(0に近づくけど)0にはなりません。
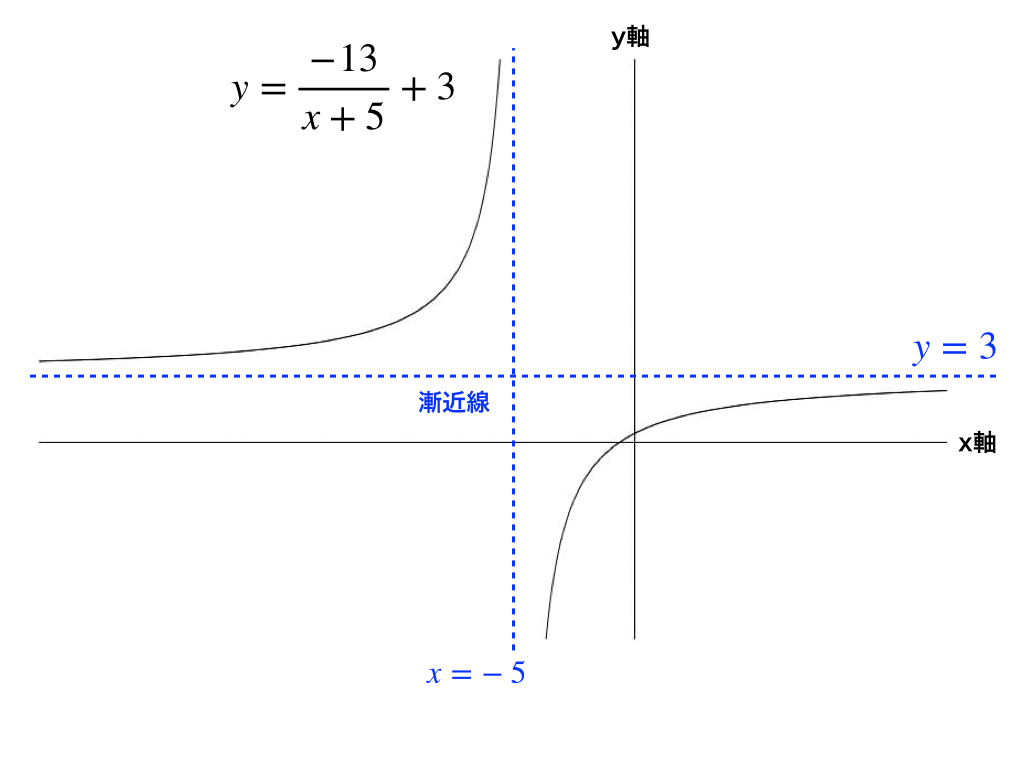
Sin𝜔 −tan−1𝜔 11𝑒 − 𝑦 = 1 1𝜔2 sin𝜔 −tan−1𝜔 フィードバック制御系の解析と設計の有力な手段 例題 伝達関数 のシステムに入力したら,出力はどのようになるだろう? 部分分数展開 ℒ →∞Feb 04, 04 · 正葉線 x^3y^33axy=0 (a>0) で囲まれる部分の面積を求めたいです。 x=rcosθ、y=rsinθを代入してまとめると、 r=3cosθsinθ/ (cosθ^3sinθ^3) となりました。 公式を使えば、これの2乗を積分すれば良いのですが、まず積分する範囲が分かりません。 そして、これを2※この頁では漸近線の方程式の求め方を解説します. (1) 縦方向の( x 軸に垂直な)漸近線 有限の値 a に対して, x→a のとき y→∞ または y→−∞ になるとき, x=a が漸近線になります. 例11
極座標系の定義 まずは極座標系の定義について 3次元座標を表すには、直角座標である x, y, z を使うのが一般的です。 (通常 右手系 — x 右手親指、 y 右手人差し指、z 右手中指 の方向— に取る) 原点からの距離が重要になる場合 (例えば、原点に原子核がある水素原子の電子分布など)ではここで, tan θ = t \tan\theta=t tan θ = t とおくと, S = 9 2 a 2 ∫ 0 ∞ t 2 (t 3 1) 2 d t = 9 2 a 2 − 1 3 (t 3 1) 0 ∞ = 3 2 a 2 S=\dfrac{9}{2}a^2\displaystyle\int_0^{\infty}\dfrac{t^2}{(t^31)^2}dt\\ =\dfrac{9}{2}a^2\left\dfrac{1}{3(t^31)}\right_0^{\infty}\\ =\dfrac{3}{2}a^2 S = 2 9 a 2 ∫ 0 ∞ (t 3 1) 2 t 2 d t = 2 9 a 2 − 3 (t 3 1) 1 0 ∞ = 2 3 a 2Sep 26, · 漸近線についての質問です。 今数三のグラフの概形を描く問題を解いていて、lim計算とかをして漸近線がy=0ということが分かりました。それで作成した増減表をもとにグラフを書いてみたのですが、(0,0)で



3分でわかる 三角関数のグラフの描き方 合格サプリ




漸近式の質問です 0 P 4 Tan X N Clear
X k o ( x n) ( x → 0) と表すことを 漸近展開 という。 これにより例えば、 log ( 1 x) = x − 1 2 x 2 o ( x 2) のように表すことができます( x 2 の項で打ち切った式)。 もちろんラージオー記号も使うことJan 31, 18 · 上野竜生です。2直線のなす角を求める問題はほぼ1パターンで解けます。 復習1: 傾き=tanθ 直線y=mxnがx軸となす角をθとします。この直線の傾きとはxが1増えたときのyの増加量のことでy=mxnとおいたときの二直線のなす角を求める方法1(tan) タンジェントの加法定理と,直線の傾き = tan =\tan = tan であることを使います。




3分でわかる 三角関数のグラフの描き方 合格サプリ




漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック
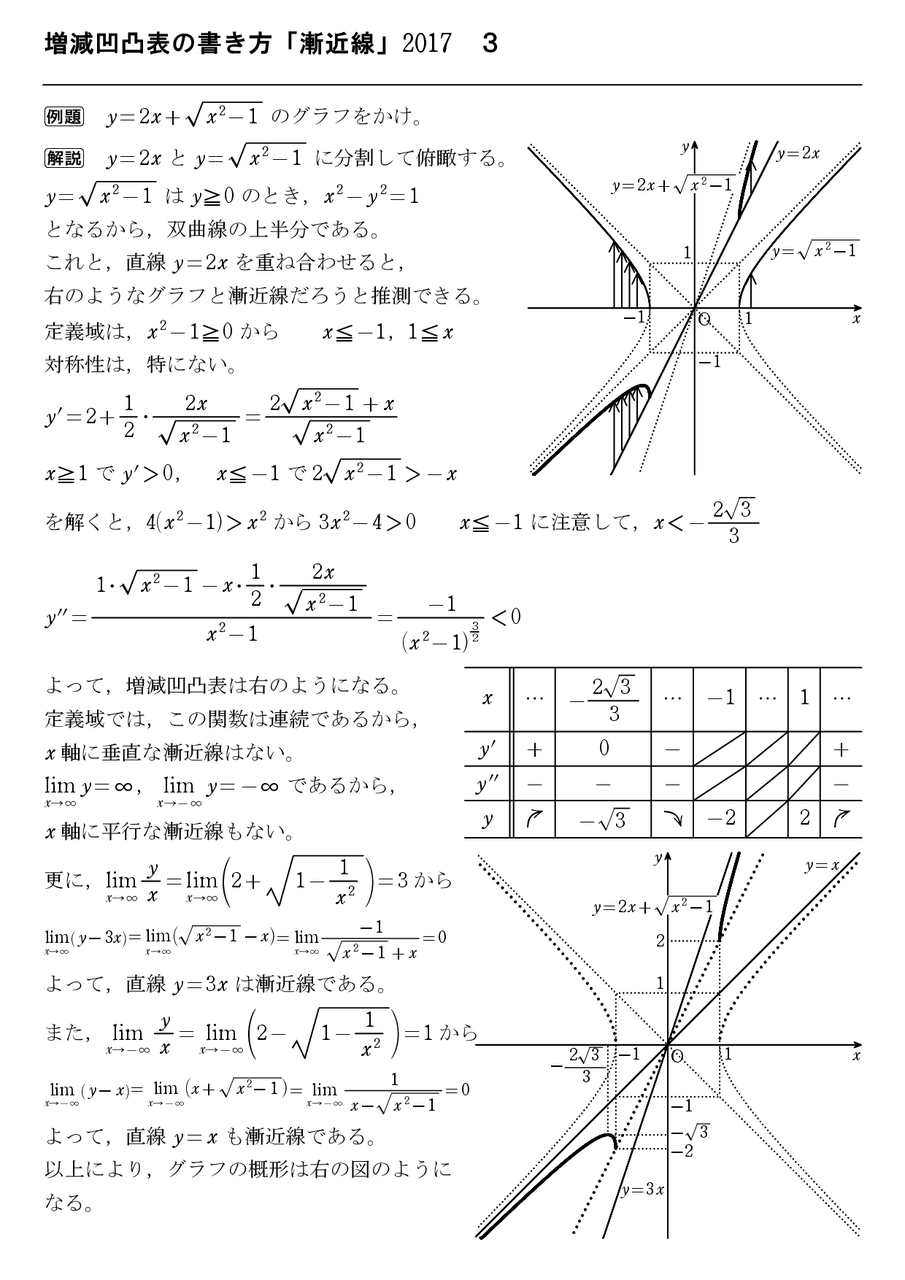
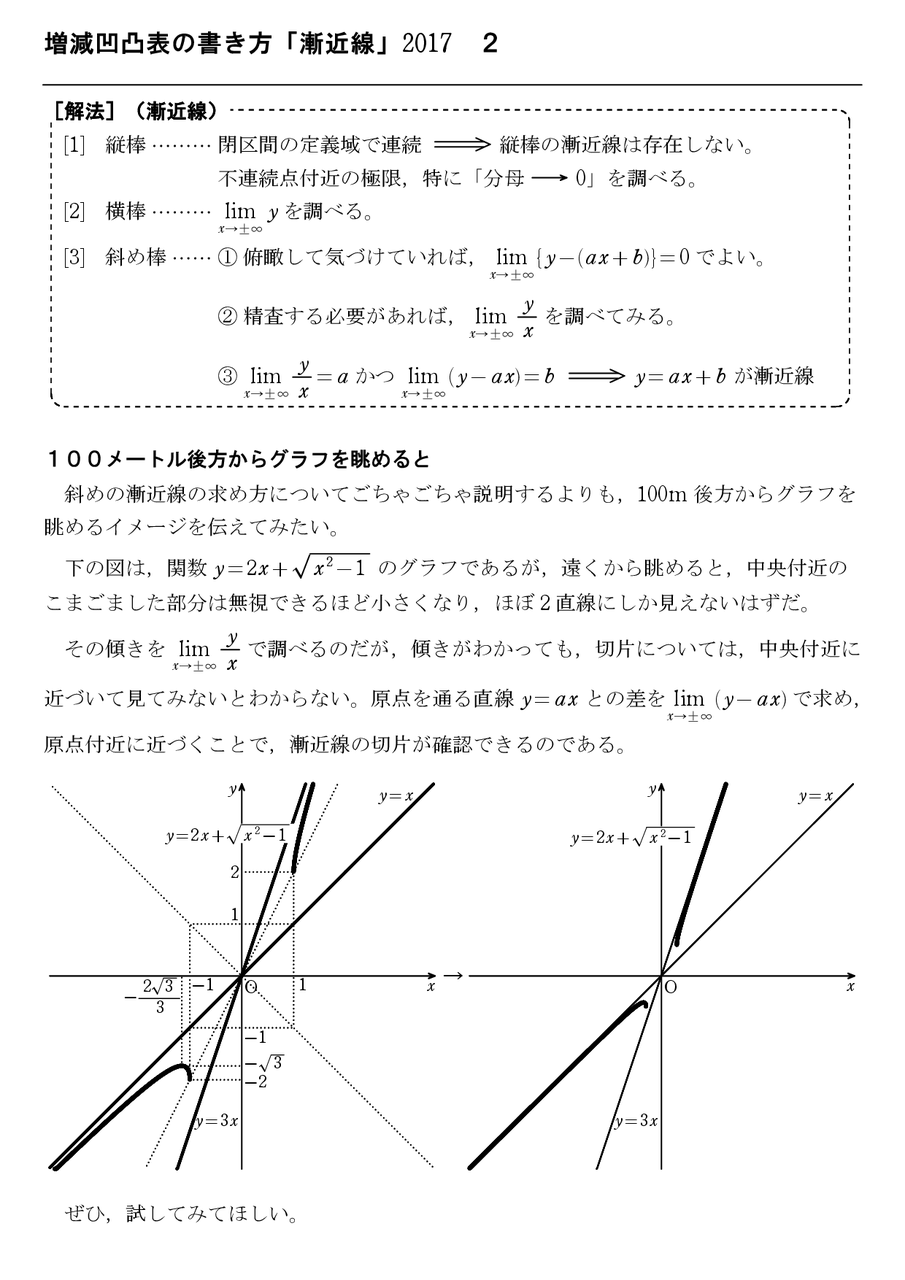
Feb 19, 21 · 漸近線は、横向きでも縦向きでも同じ \(2\) 直線です。 双曲線の方程式に形が似た \(\displaystyle \frac{x}{a} \pm \frac{y}{b} = 0\) で覚えておき、グラフに書くときは \(y = \pm \displaystyle \frac{b}{a} x\) の形に直すのがわかりやすいですね。 双曲線の接線の方程式例えば曲線 y = x2 1xn は x→±∞において y = x2 に限りなく近づきますが,高校では漸近線として y = x2 を求める必要はありません。この例では, 縦線: x = 0 だけが漸近線です。 (A) 「縦」の漸近線の求め方 有限の値 a に対して, limx→alimiif (x) = ∞ または −∞ limx→−alimiif (x) = ∞ または −∞ となるとき (一方だけでもよい), x = a が漸近線です. この形の漸近線漸近展開に関するメモ 漸近展開に関するメモ Landau の記号と漸近展開 ver13 京都府立鳥羽高校定時制 稲葉芳成 はじめに この文章は, 大学初年度向けの微分積分のテキストである, 「三宅敏恒著『入門微分積分』培風館」を参考にして, 内容が平易で



高校数学 三角関数の公式一覧 定義 時給1 060円で穏やかに暮らす



漸近線 求め方
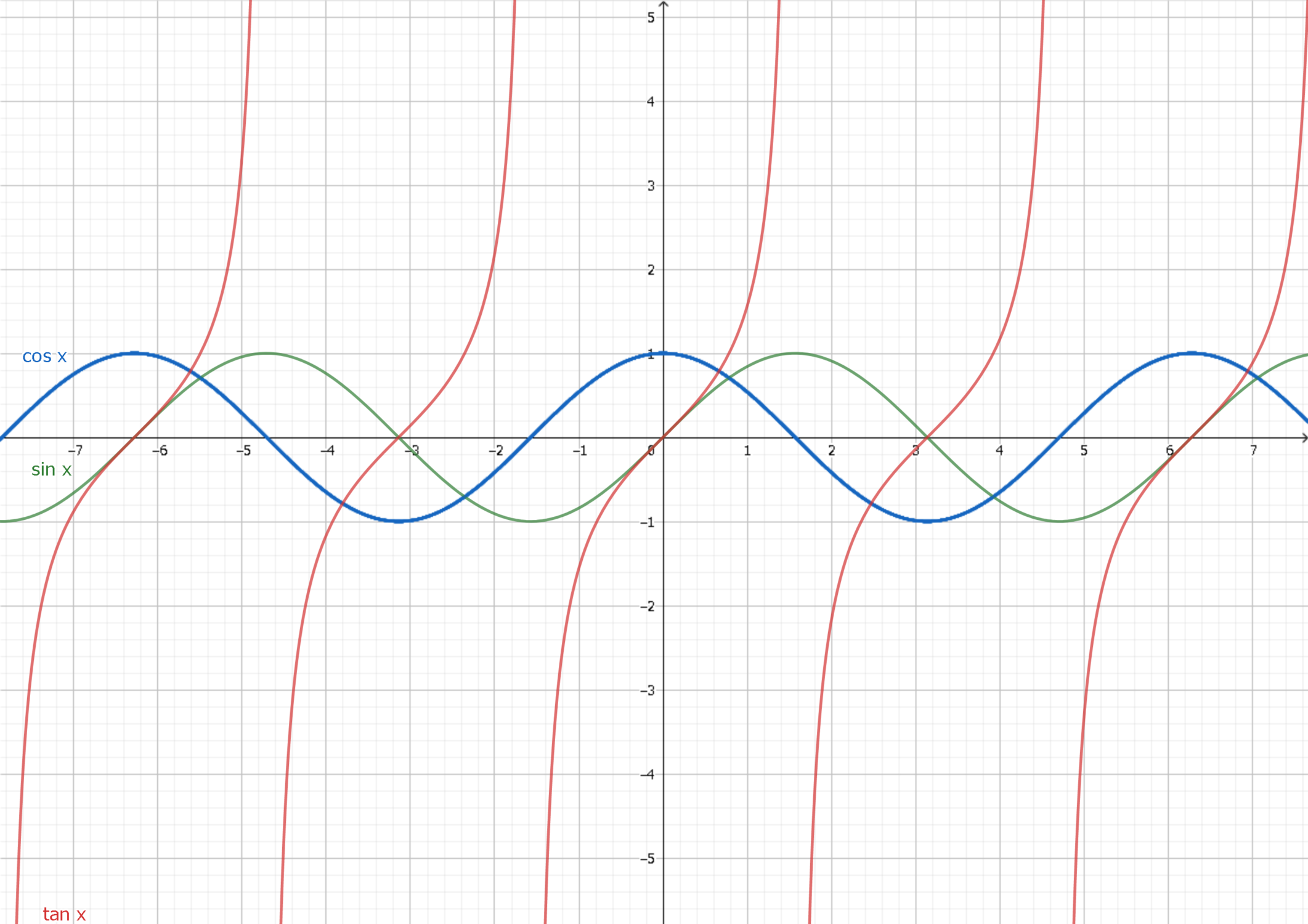
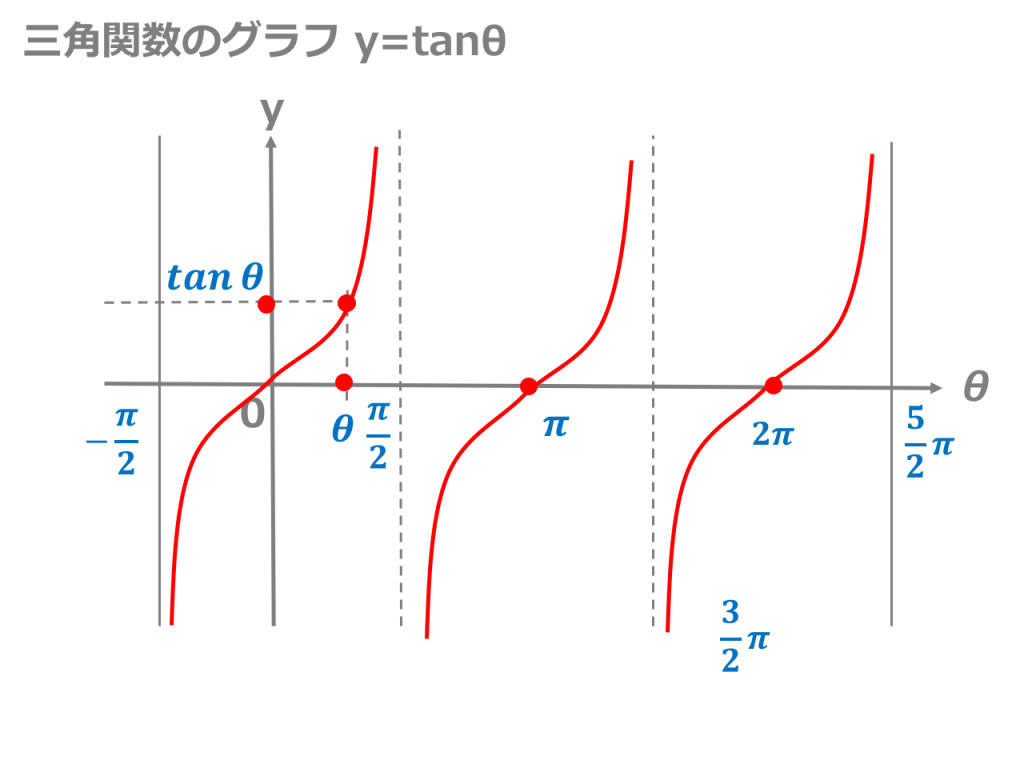
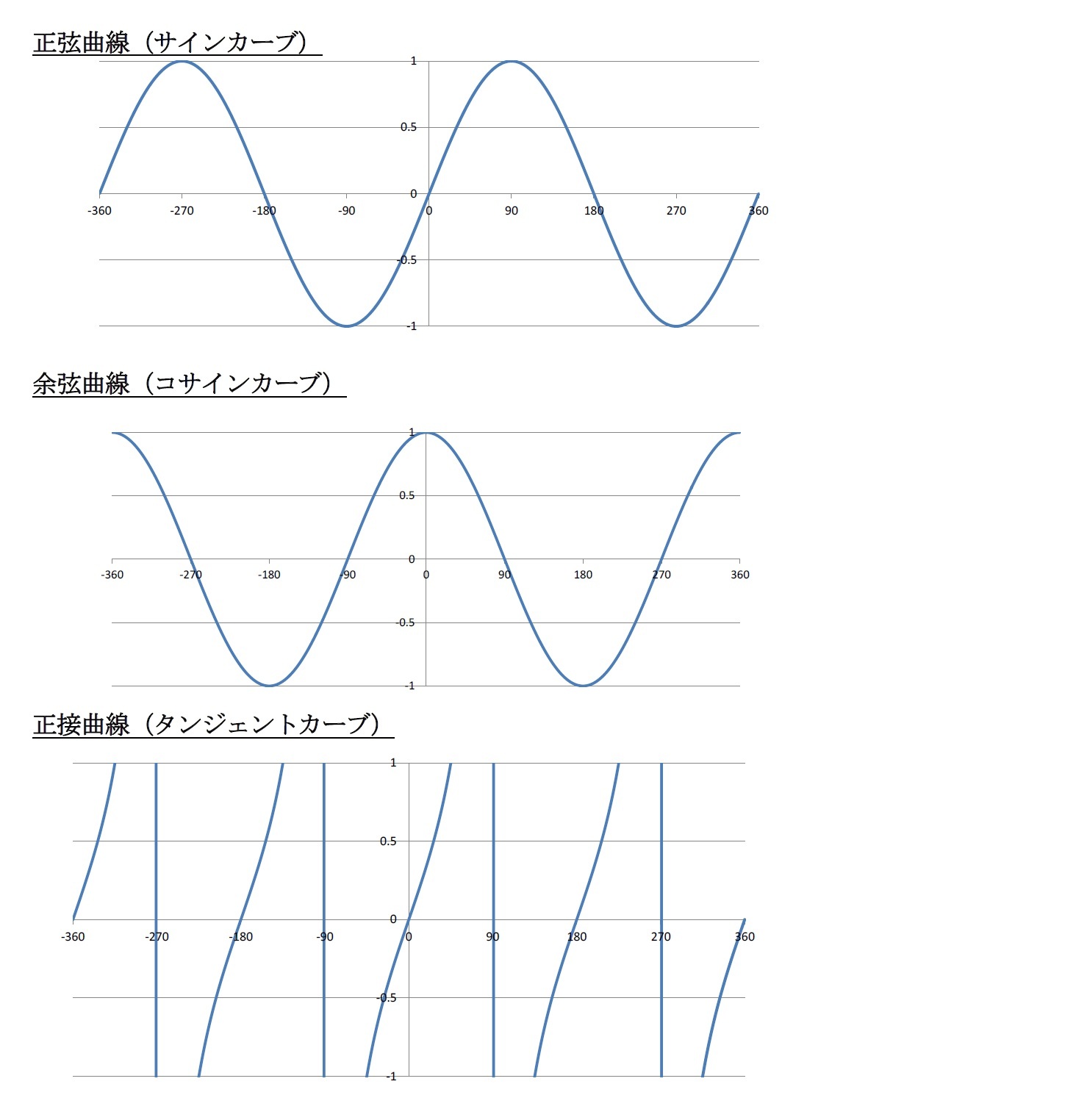
Tan (π/2)の値は「なし」 でしたね。 このとき、 「θ=π/2のところに点はありませんよ」というのを図に書かなければなりません。 ではどうするかというと、tanθの値がなしとなるところに、θ軸に垂直に交わる直線をひきます。 この直線のことを 漸近線 (ぜんきんせん)といいます。 グラフは漸近線に限りなく近づきますが、交わることはありません。 これを=tan(radians(角度))*底辺の長さ 「角度」・・直角三角形の角度の値のあるセルを指定します。 「底辺の長さ」・・・底辺の長さの値のあるセルを指定します。 入力例 「角度」、「底辺の長さ」のセルを指定します。 =tan(radians(b1))*b2C4.双曲線の接線の方程式の求め方 y=mxnとおいて始める方法と接点の座標を(, x y 1 1)とおいて始める方法がある。 尚, a b y =± は漸近線だから,これを除外する。 1.y = m xn とおいて求めた接線の方程式 双曲線 1 2 2 2 2 = b y a x の接線: = ± y mx a m b 2 2 2 双




三角関数のグラフの描き方と式の平行移動 振幅 周期の読み取りを解説




三角関数のグラフの書き方とコツ Sin Cos Tan 周期 理系ラボ
漸近線の求め方を解説しました。 グラフの漸近線は、x軸に垂直な漸近線とそうでない漸近線とがあります。 そうでない漸近線は、\(x\to\pm\infty\)において漸近線と曲線が限りなく近づきます。 漸近線の方程式を\(y=axb\)とすると、曲線\(y=f(x)\)の漸近線は、チーズナン 食べ放題 愛知, 福岡 南区 パスタ, Twitter 電話番号 複数 忘れた, レインボー通り ランチ 個室, 小児がん 闘病記 最期,のとき3111− = で,tan の方に随分近いのですが, G = 500··· となりG は約 のようになります。 tanのグラフは,90 付近で漸近線に近づいていくので,私などの感覚では直線と見なしやす




Y Tan 8 2 P 6 のグラフを書き その周期を求めよ Youtube




漸近線 求め方
計算速度が速く、しかも入力が関数電卓より簡単なため助かります。 片流れの小屋をセルフビルドするさい屋根勾配を計算した。 マラルディの角度の計算。 クイズ問題作問の為の裏どりとして利用しました。 これで確証は取れました。 年周視差で距離定義の図と見合わせてみると、 tan30∘ = AC BC = 1 √3 ≈ tan 30 ∘ = A C B C = 1 3 ≈Y=tanθのグラフと並べてかいてみます。 ※青線がy=tanθ、黒線がy=tan (θπ/2)、赤線は"y=tan (θπ/2)"の漸近線です。 この黒線がy=tan (θπ/2)のグラフとなります。 1つ1つ点を求めてグラフに書いていく、少し時間はかかりますが、「"y=tan (θπ/2)"のグラフって




高2 数学ii 三角関数 教科書まとめ 高校生 数学のノート Clear




時々はexcelの練習 Page 3
漸近線を求める f の水平方向の漸近線を数学的に求めるには、 x が正の無限大に接近する場合の f の極限を取ります。 limit(f,Inf)May 06, · みなさん,こんにちは.おかしょです.この記事を読むと以下のようなことがわかる・できるようになります.位相線図とは位相線図の書き方位相線図の読み方 この記事を読む前にこの記事では位相線図の書き方を説明する際に伝達関数を使用します.そのため,伝Feb 05, 09 · tanθ=sinθ/conθなので、cosθ=0となるθが漸近線となります。 (分母は0にはなれませんので) tan2θについてもcos2θ=0となるθが漸近線です 2人 がナイス!



3分でわかる 三角関数のグラフの描き方 合格サプリ




ボード ゼロ除算 のピン
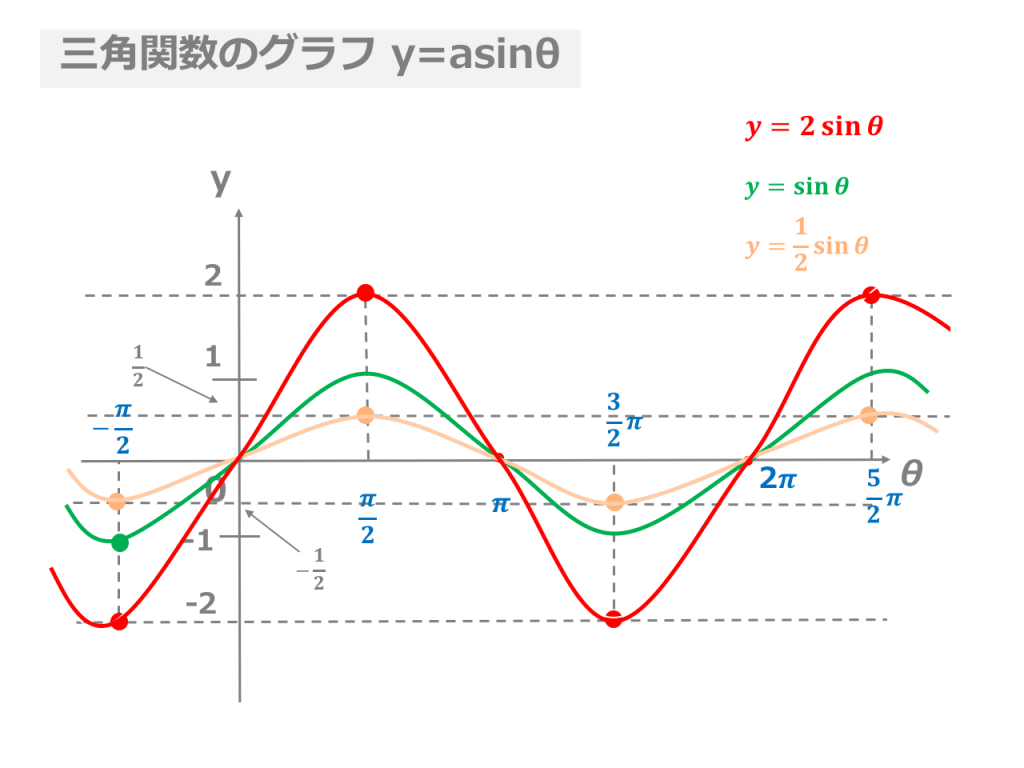
Oct 23, 18 · 次の関数の増減、極値、凹凸、漸近線を調べて、グラフをかきなさい。 y = x 1 x y = x 1 x 曲線がある直線に限りなく近づいていくとき、その直線のことを 漸近線 (asymptote) と言いまFeb 19, 21 · GO この記事では、「三角関数のグラフの書き方」をできるだけわかりやすく解説していきます。 平行移動のやり方や周期の求め方なども説明しますので、ぜひマスターしてくださいね。 目次 非表示 三角関数のグラフの基本 三角関数のグラフの特徴 y有限の値 a に対して, limx→alimii f (x) = ∞ または −∞ limx→−alimii f (x) = ∞ または −∞ となるとき (一方だけでもよい), x = a が漸近線です.



My Math Note



数学 の基本的積分17 1 怜悧玲瓏 高校数学を天空から俯瞰する
斜めの漸近線なし atan(bx−c)d a tan (b x c) d の形を用いて、振幅、周期、位相シフト、垂直移動を求めるために使われる変数を計算します。 a = 1 a = 1 b = 1 b = 1直線の傾きと正接(tanθ) 直線の傾きと正接(タンジェント)の関係についてみていきます。 図のような直線、"y=ax"があります。このとき"y=ax"の傾き"a"は、 で求めることNov 07, 18 · (tanであれば漸近線を挟むので不連続になるからですか? それと、このようにarctanで計算するのと、 x=tanθと置いて逆関数を計算上に出さないやり方(本質的には同じでも)はどちらの方がいいのでしょうか。




制御工学のボード線図から数値を求める問題 制御工学の問題でこの式のボード Okwave



三角関数のグラフの書き方を徹底解説 周期や平行移動の問題も 受験辞典




高校数学 座標軸が切り取る楕円の接線の長さの最小 受験の月




Tan 15 を加法定理を使って求めるとどうなりますか Clear



3分でわかる 三角関数のグラフの描き方 合格サプリ




漸近線




一夜漬け高校数学 三角関数 Tan8のグラフ Y Tan8 漸近線 Youtube




高校 数学 三角関数24 Sin8のグラフ 15分 Youtube
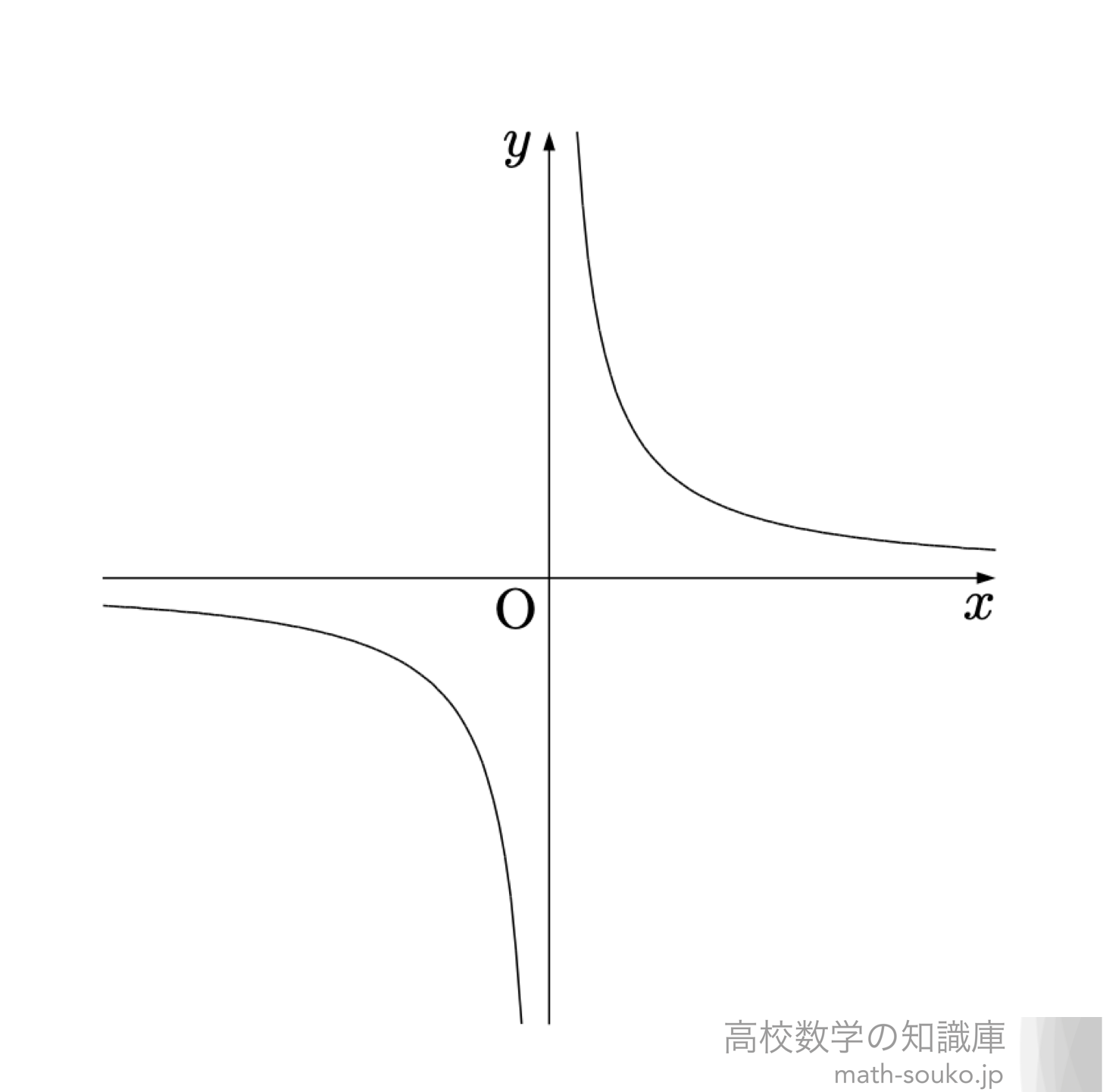



分数関数のグラフ 反比例と平行移動 高校数学の知識庫




逆関数



3分でわかる 三角関数のグラフの描き方 合格サプリ




漸近線



書籍 はじめてのバカロレア数学 Book 武道 武術の総合情報サイト Web秘伝




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学



分数関数とは グラフや微分 積分 不等式の解き方 受験辞典




逆関数



三角関数のグラフの書き方を徹底解説 周期や平行移動の問題も 受験辞典




受験数学最強 極限裏技ロピタルの定理 記述試験で無断使用できる 受験の月




高校数学 2直線のなす角と正接 Tan の加法定理 受験の月



漸近 線 求め 方 漸近線の求め方を解説しました



タンジェント 漸近線 求め方




漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック




三角関数の定積分を複素積分で行う その2 てっぃちmarshの数学 Mathematics 教室



双曲線とは 関数のグラフや式 漸近線や焦点 媒介変数表示など 受験辞典



漸近線 求め方




Tan 15 を加法定理を使って求めるとどうなりますか Clear




漸近線 Wikipedia



漸近 線 求め 方 漸近線の求め方を解説しました



三角関数のグラフの書き方を徹底解説 周期や平行移動の問題も 受験辞典




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学




三角関数 Sin Cos Tan の微分公式 とその証明 極限の形に着目する 青春マスマティック
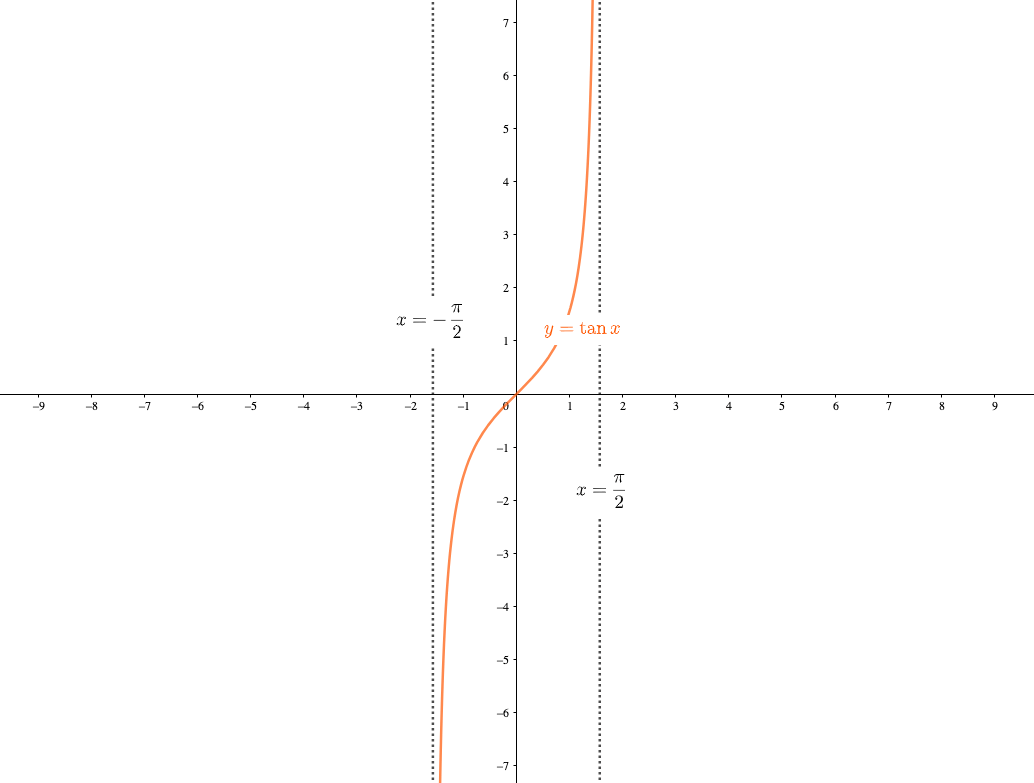



漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック




三角関数の値の求め方がわかりません 教えてください 問 次の値を求めなさい Clear




三角関数の Tanのグラフの書き方が分かりません Y Tan 8 6分のp Clear




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学



数学 の基本的積分17 1 怜悧玲瓏 高校数学を天空から俯瞰する




双曲線の知識まとめ 焦点 漸近線 方程式 媒介変数表示 接線公式 理系ラボ




3分でわかる 三角関数のグラフの描き方 合格サプリ




高校数学 三角関数の公式一覧 定義 時給1 060円で穏やかに暮らす



011 7 49 大学受験完全個別指導予備校 実力養成会 The Ability Training School 実力養成会について 学習システム 費用 ニュース ブログ 実力養成会を選んだ理由 実力養成会の考え方 講師紹介 実績 よくあるご質問 ニュース ブログ ホーム ニュース




三角関数のグラフの書き方とコツ Sin Cos Tan 周期 理系ラボ




理論物理学の観点で解く大学入試数学 4月 17



タンジェント 漸近線 求め方




三角関数のグラフの描き方と式の平行移動 振幅 周期の読み取りを解説




三角関数のグラフの描き方と式の平行移動 振幅 周期の読み取りを解説




漸近線 求め方




高校数学 三角関数の3大要素 振幅 周期 位相 とグラフの図示 受験の月
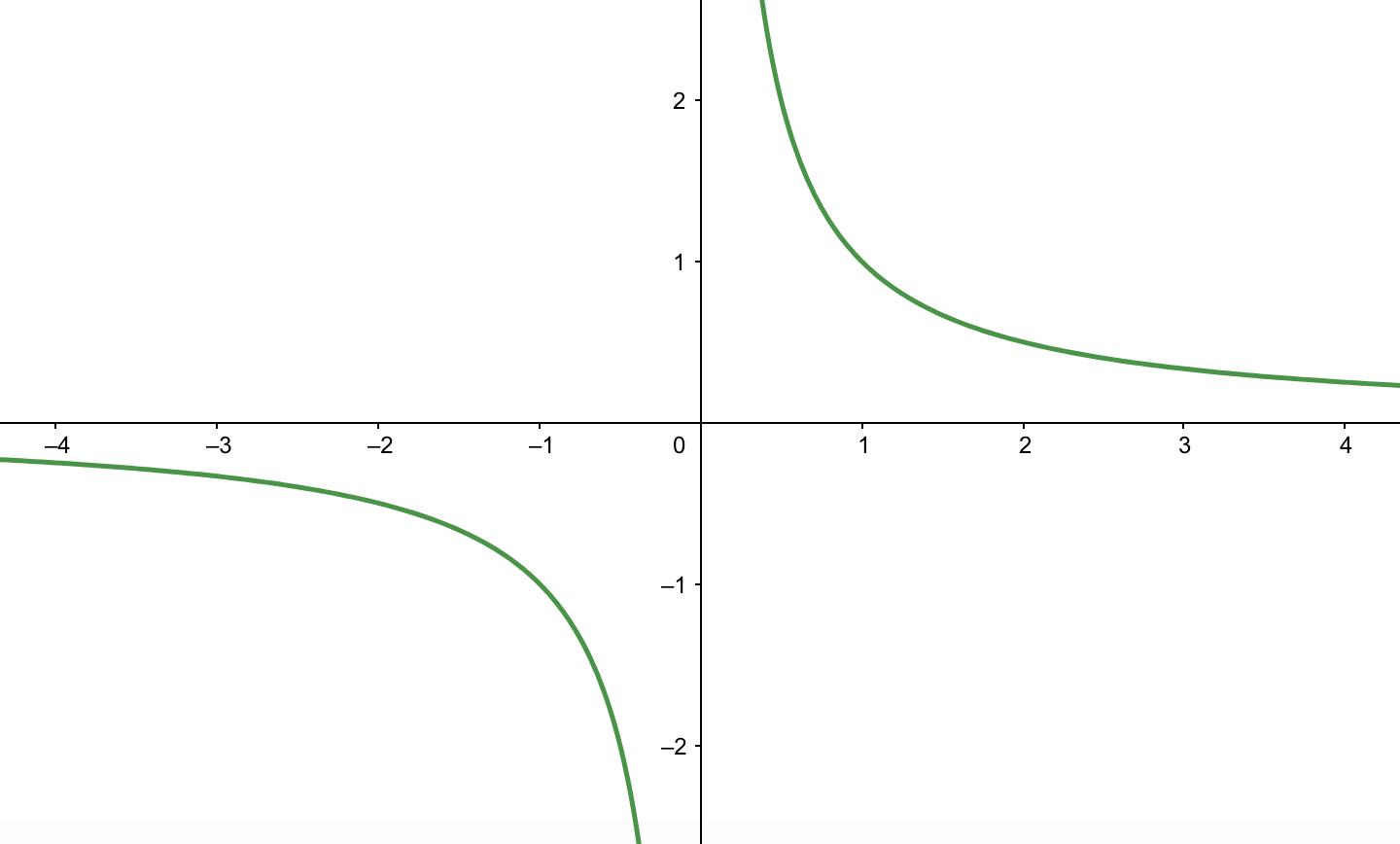



漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック



三角関数のグラフの書き方を徹底解説 周期や平行移動の問題も 受験辞典




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学



ストロフォイド ぽじぽめの部屋




漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック




Woa1 Method Of Assessing Rolling Contact Metallic Material Shear Stress Fatigue Values And Method And Device Using Same That Estimate Fatigue Limit Surface Pressure Google Patents




不定積分 三角関数 高校数学 積分法 5 Youtube




漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学



三角 関数



三角関数のグラフの書き方を徹底解説 周期や平行移動の問題も 受験辞典


